Resizing images using seam carving method

📚 Technology Stack

C/C++, Cuda, Parallel Programming

📃 Seam carving

It operates by establishing a number of seams (the least important paths) in an image and automatically removing the seams to reduce the size of the image or inserting connections to expand it. In this project, the goal is to remove the least important seams.

The purpose of the algorithm is to align objects in the image, display the image without distortion on different sized devices (mobile phones, large screens).

---

Input: an RGB image with size [W, H, 3] and the number of seams to be removed N

Output: an image with N seams removed in the width direction, size: [W-N, H, 3] without distorting important objects.

Steps to perform basic seam carving algorithm

Convert image to .pnm if it is not in the correct format

Process

• Compute weight/density/energy for each pixel.
  • Convert the image to grayscale.
  • Blur the image using Gaussian Blur.
  • Detect edge points using Sobel Filter.
  • Build Energy Map from the edges along the horizontal and vertical directions, respectively.
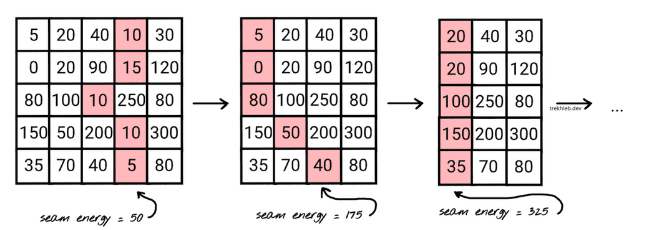
• From the Energy Map, construct a list of seams. Seams are sorted by energy, where seams with low energy are considered less important for the image content. Seams can be computed through the dynamic programming approach.
• Remove the required low-energy seams.

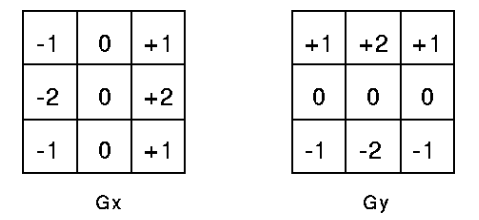
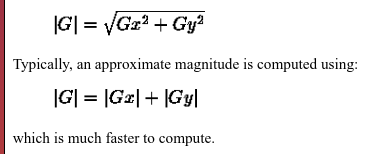
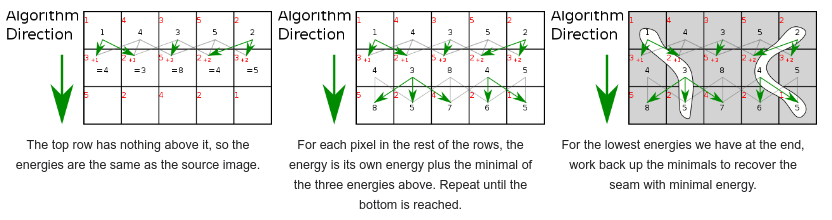
Algorithm analysis for finding the path with the least energy

Calculating a seams line involves finding a line with the lowest energy cost from the top to the bottom of the image. This can be achieved through algorithms such as Dijkstra, dynamic programming, or greedy...

Dynamic programming is a programming method that stores the results of sub-calculation to simplify the computation of a complex result. Dynamic programming can be used to calculate seams lines. If we try to calculate the vertical seam with the lowest energy, for each pixel in a row, we calculate the energy of the current pixel plus the energy of one of the three possible pixels above it.

The implementation of finding seams using dynamic programming is used. Let F[i][j] be the minimum energy of seams ending at pixel[i][j]. From there, we have a simple recurrence formula as follows.

F[i][j] = min(F[i+1][j-1], F[i+1][j], F[i+1][j+1]) + e[i][j]

At each row, compute each value in the row of the temporary matrix according to the dynamic programming formula.

At each step, the trace matrix[i][j] stores the index value of argmin(F[i+1][j-1], F[i+1][j], F[i+1][j+1]) to track the optimal value of the seams.

Installation step by step

Comment

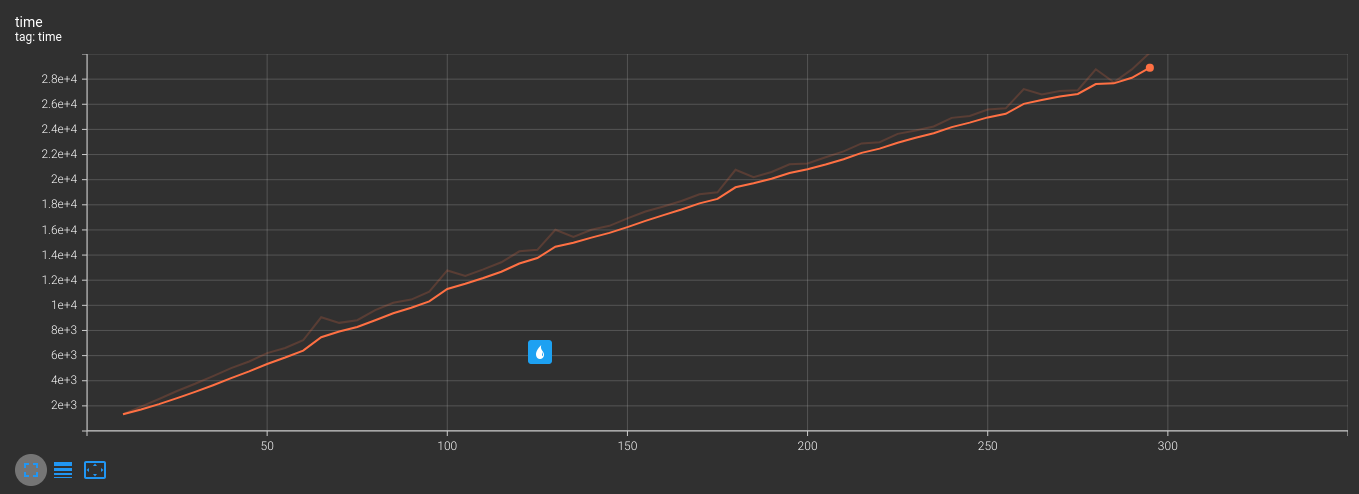
We can see a graph between the number of seams removed and the time taken to create almost a bisector of the first quadrant angle. This means that when we need to remove twice the number of seams, the execution time also increases by almost twice. This is quite bad. This is because the Seam-Carving algorithm has a large complexity when executed sequentially because most of the steps in the algorithm have a complexity of O(n^2). For example:

• Converting the image to grayscale takes O(n^2), as each pixel is processed independently.
• The convolution steps (blurring the image, finding edges, constructing the energy map) take O(n^2) to perform convolution on each image pixel.
• The dynamic programming step of finding the seam with the smallest importance or removing a previously found seam both have a complexity of O(n^2).
• Removing seams takes O(n^2), with each row being processed independently. Similar to copying a matrix but not counting pixels that belong to removed seams.

It can be concluded that applying parallel computing in this problem is very appropriate since most of the main steps of the algorithm can be parallelized.

Version 1

---

In the first parallel version, we implemented parallelization as follows:

• Parallelize the conversion of images to grayscale
• Parallelize convolution functions directly from GMEM
• The host performs dynamic programming calculations
• The host performs finding the smallest value seams in N seams
• The host performs sequential backward tracing based on the traceMap array to find this seam (or the pixels to be deleted)
• Parallelize the deletion of pixels by flattening the input array, copying the elements that are not on the seam to the output array

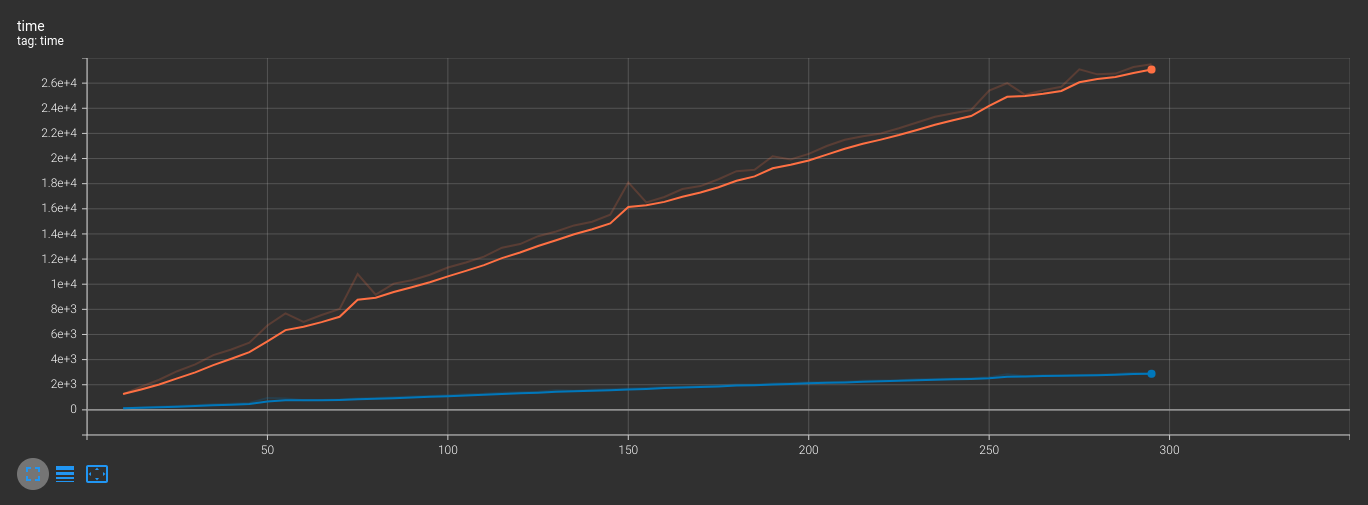
• For the blur steps, we used convolution to find features in parallelization. Our group used SMEM to speed up the algorithm.

Comments

After testing the parallel computing part, we realized that the time to copy data from host to device and from device to host is quite significant. Therefore, when running with a large number of seams using the device, the running time becomes less efficient.

For a small number of seams (equal to 10), the power of parallelization will be demonstrated. However, when the number of seams increases, the performance of this optimization is equivalent to the basic version.

The reason why SMEM is faster in some cases is because SMEM is located on the SM → with much faster access speed than DRAM (GMEM). Data will be copied to the SMEM of the same block before convolution, and the threads will use this shared data → increasing the speed.

Version 3

---

For the third parallel version, we parallelize as follows:

• For the dynamic programming step of finding the least important seam, parallelize on each row instead of sequentially for each pixel

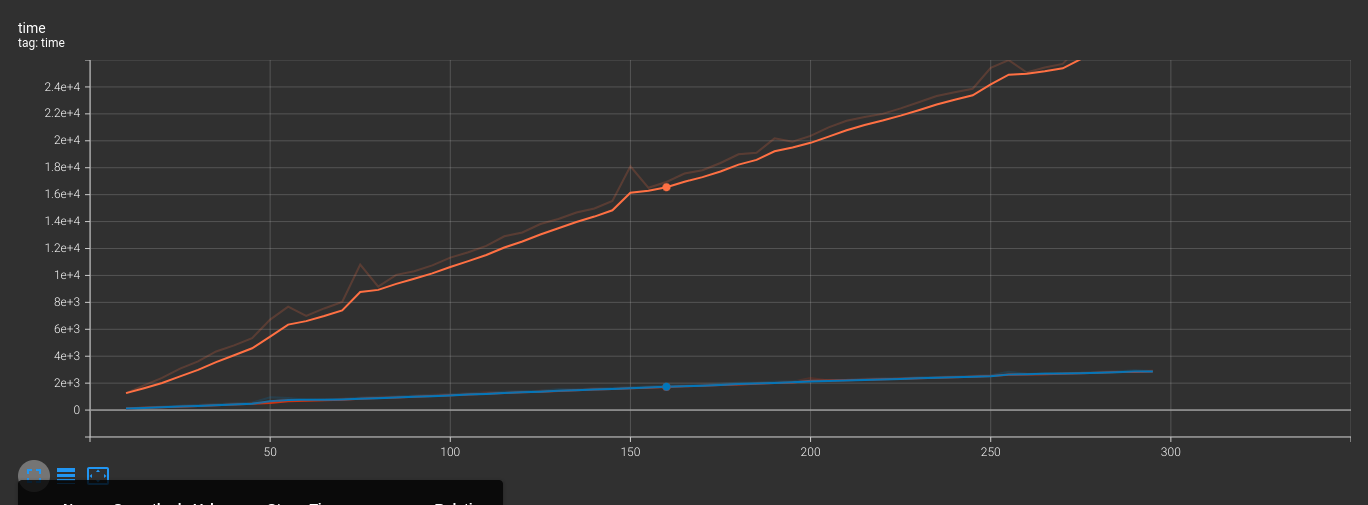
Comments

• When parallelizing the steps, the seam-carving algorithm has significantly improved its execution time compared to the previous 2 versions.
• In terms of ideology when parallelizing, the team did not change the original ideology and the parallelized version still significantly improved the time.

Development direction

• We can optimize by using the idea of two-end BFS, from which we can calculate in two directions from top to bottom and from bottom to top, and then synthesize the results by taking the smallest total result of the row. It is easy to estimate that the algorithm speed will decrease by half. F[n/2]+F[n/2+1]
• Currently, the main direction of the group is to optimize the time for one algorithm execution. However, in practice, when using the algorithm to measure performance, we always want to maximize the number of seams that can be run. This is the biggest limitation to the idea of optimizing the algorithm, making the algorithm unfavorable. A proposal may be to use one image in each deletion and perform only one deletion on the returned result.
• This idea can also apply the Forward Energy method at http://cs.brown.edu/courses/cs129/results/proj3/taox/, which helps us not have to recalculate the energy step. Forward Energy predicts which pixels will be adjacent after removing the seam and uses that to suggest the best seam to remove. This is in contrast to backward energy. For the old algorithm, the formula for calculating the minimum energy of a pixel is based on the three adjacent pixels above. This will be a major obstacle if all 3 pixels have similar values, leading to the removal of the seam (point with the smallest energy) and unintentionally removing an important part of the texture in the image.